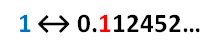home | what's new | other sites | contact | about

Word Gems 

exploring self-realization, sacred personhood, and full humanity

Editor's 1-Minute Essay:

 Eternity and Infinity

return to "Eternity and Infinity" main-page

“If the doors of perception were cleansed every thing would appear to man as it is, Infinite. For man has closed himself up, till he sees all things thro' narrow chinks of his cavern.” William Blake

Editor's note: The purpose of this article is to offer a brief outline of the historical development of the concepts of "eternity" and "infinity." The discussion below is divided into five major sections: 

I.  A condensed summary of Dr. Mortimer Adler's Syntopicon essays on Eternity and Infinity

II.  Georg Cantor on infinity -- one of the most powerful ideas of history: some infinities are bigger than others

III.  Dr. William Barclay's explanation of the New Testament Greek word for "eternal" life

IV. Eckhart Tolle and the "eternal now"

V.  Conclusion and Summary Thoughts

I. Dr. Mortimer Adler's Syntopicon essays on Eternity and Infinity

Dr. Adler, one of the great teachers, often featured on the Word Gems site (see, for example, Education and Philosophy), wrote 102 essays on what he called "the great ideas," concepts featured in the writings of leading thinkers of the last 2500 years.

I've abstracted from Dr. Adler's Syntopicon essays the essence of what notable writers have said about Eternity and Infinity since the time of Plato.

Adler: “The notion of eternity, like that of infinity, has two meanings.” Leading thinkers of history have conceived of eternity within the following two broad definitions:

Eternity #1: an infinite-duration concept with reference to time as an endless succession of moments; also called the “eternity of time”; this flow of interminable present-moments – which some consider to be the definition of time -- allows for change and motion, for, as ancient thinkers have pointed out, without time there can be no change or motion.

Eternity #2: an infinite-duration concept that does not reference time as a succession of moments and, with this denial of the temporal, precludes change and motion; instead, within this definition, there is the view of an “eternity of now,” a single eternal timeless moment.

This concept of eternal immutability (definition #2) is related to, came to be incorporated into, Plato’s Ideal Forms and Aristotle and Aquinas’ God as “Unmoved Mover.”

Augustine speaks of God as inhabiting “ever-fixed Eternity” (definition #2): “Thy years are one day, and Thy day is not one day but To-day … Thy To-day is Eternity.”

Aquinas said that “eternity (definition #2) is the proper measure of being” – because he assumed that a changeless state implied perfection – while time (definition #1) is the proper measure of movement” in the physical world.

Plato spoke of these two major concepts of eternity in terms of changeless being (definition #2) and an in-flux becoming (definition #1). He said that the notion of “is” belongs to eternity (definition #2) but “was” and “will be” exist only in time (definition #1).

These concepts of eternity influenced RCC doctrine, in that, the afterlife was conceived as a place of no-time (definition #2). Therefore, it was taught that moral change and growth is not possible in the next world. We now know this view to be absolutely wrong.

The two meanings of eternity – endless succeeding moments of time (definition #1) and unchanging timelessness of being (definition #2) carry over into the discussion of infinity. According to many thinkers, infinite being is akin to absolute perfection (definition #2).

Adler: “But in the field of quantities other than time, the meanings of infinite and eternal part company… The consideration of space and number leads us to an aspect of infinity which has no parallel in the consideration of eternity."

Pascal: “In sizes or numbers, nature has set before man two marvelous wonders” – the infinitely large by endless addition [of one more], or the infinitely small by endless division; you can always add one more, and you can always divide a fraction into halves, no matter how small the fraction might be.

Adler: We have “paired notions of the unlimited and limits approached but not attained” -- that is, regarding the latter, when dividing smaller and smaller fractions, we can never actually get to zero.

Adler: “While it is impossible for there to be two infinite beings (i.e., two Gods), it is not impossible for there to be two, or more” – or any number of – “infinite quantities.”

Adler: “To man alone, among all admittedly finite things, has infinity been attributed … [It is] “with regard to capacity that some thinkers have attributed man’s infinity … According to the theory of natural desire, the tendency of each nature is somehow proportionate to its capacity. If man’s restless search for knowledge and happiness can be quieted only by the possession of the infinite truth and goodness of God, then man’s intellect and will must somehow be as infinite in nature as they are in tendency.”

II. Georg Cantor's view of infinity, one of the most powerful ideas of history:

some infinities are bigger than others: 'countable' and 'uncountable' infinite sets

Prepare to enter a world of weirdness. The following concepts might rank among the most counter-intuitive we'll meet on this planet.

We know of finite sets: the number of eggs in a carton, the number of children in a classroom, the number of books in your city's library. All these sets are finite. We might even throw into the mix the number of grains of sand on all of the beaches in the world - a very large number, but still finite.

enter the infinite set

But there are other sets which are infinite in number. For example, the set of all counting or natural numbers. We begin with 1, 2, 3, 4, 5 ... and we go on forever adding one more to this list.

The counting numbers represent an infinite set. We see this. So far so good.

But there are other closely-related infinite sets, such as the set of whole numbers which is equal to the "natural numbers" but for zero added to the front: 0, 1, 2, 3, 4, 5 ... continuing on forever.

And then there are the integers, which include the just-mentioned whole numbers plus all of their negative counterparts: 0, 1, -1, 2, -2, 3, -3, 4, -4 ... continuing on forever.

And let's not forget the fractions. All of the integers, including zero, can be expressed as a fraction; for example, 1/1, 2/1, 3/1... on and on. But this is only part of the story as, to be thorough, we have to include every fraction, every little-bitty fraction, on our list if we want to have a complete list. Mathematicians have devised the following diagonal method to ensure that every last fraction will be on our list, including 1,456 / 89,678 along with 284,848 / 3,408,278.

The "3 dots" -- vertical, diagonal, and horizontal -- indicate "going on forever."

The entire domain of the fractions is called "the rational numbers" because each might be expressed as a ratio, which is just another way of looking at a fraction, with the number on top in relation to the number on bottom.

• The entire domain of the rational numbers constitutes an infinite set. The "rationals" have to be an infinite set because, just as we can always "add one more" to any number, we can always divide anything into halves, no matter how tiny -- which is why we speak of the infinitely large as opposed to the infinitesimally small. Adding one more, or dividing into two, goes on forever. 

 All of this, pretty much, we can understand. It sort of makes sense to us. But let's take a step into true weirdness.

Mathematicians use the term "countable" or "listable" infinities. For example, we can't actually count all the elements in the set of the natural numbers but, theoretically, we can put them on a "list," on a number line, and we can see that number line going off into infinity via the process of "adding one more." We get the idea, or think we do. We can't actually see every counting number on that list, but we understand that the list will eventually contain every last one of them. It will be a complete list, albeit ever-expanding. We're almost satisfied with this.

But then we learn that there are some number lists, so large, so mammoth, that we can't even put them on this ever-expanding sort of list. These are the "uncountable," "unlistable" infinities. A "complete list" for these would be impossible and far, far bigger than any of our "countable" or "listable" infinities. So big are the "uncountable infinities", so overshadowing of our plain-vanilla "counting infinities," that we could get rid of all the "rational numbers" on the number line and we wouldn't even notice they're gone!

Now we've stepped over the threshold into the truly weird.

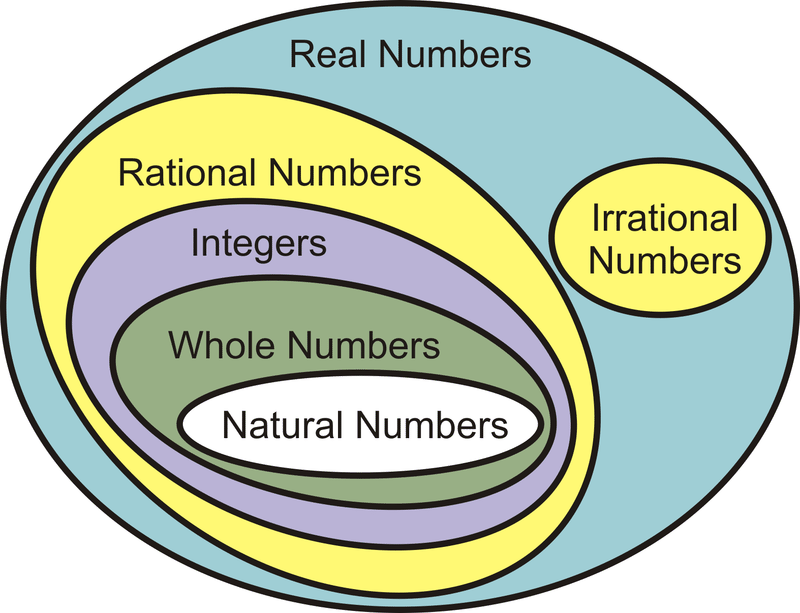
enter the uncountable, unlistable, infinite set; an infinite number of them

Have a look at this diagram of the real number system to see where we are so far:

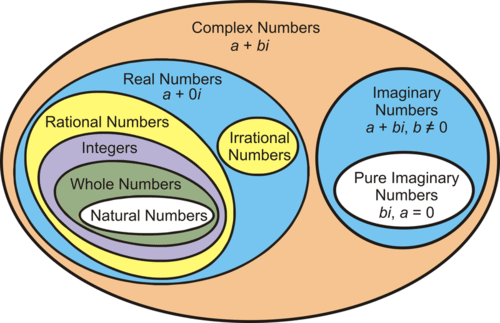
We notice the "naturals," the "wholes," the "integers," all subsumed under "the rationals."

To simplify, we might view the entire real number system comprised of two major components, the rationals and the irrationals.

Editor's note: The very term "reals" or "real numbers" is unfortunate and misleading, a misnomer. The term "real" was applied at a time when it was believed that a newly-conceived order of numbers could not actually exist and, therefore, were labeled "imaginary numbers." The "real numbers," therefore, suddenly gained the name "real" when set against the newly-discovered "imaginaries." 

The "imaginaries," however, are anything but ghostlike and are used in engineering and physics all the time. They refer to other dimensions on the coordinate plane; that is, not just "right and left" and "back and forth" on the 2-D plane but also "up and down," an ascension from, a lifting off of the 2-D plane. This is what the "imaginaries" allowed mathematicians to visualize and rocked the world of traditional Cartesian concept. It was considered heresy back then. We recall the humorous line from Flatland, "upward not northward."

Some of the terms of science are misnomers, anachronistic vestiges of less-informed times; such as the word "atom" which, errantly, denotes "indivisible," an altogether unwarranted judgment given the advent of a zoo of sub-atomic particles. "Atom" is more than label but, in fact, an editorial comment. It means to say, "we really know now, we've got it all, no new discoveries are possible, we're at the end of the line of the building-blocks of reality." But they hadn't even truly begun. It was an arrogant assessment.

The world of science is not immune from "infallible doctrine" pronouncements, the poisonous spirit of dogmatism and cultism. Any time we hear a self-appointed authority - whether, corporate, political, or religious - speaking pompously of having attained final knowledge, a last word, or infallible doctrine, we can immediately know that such herald of certainty is automatically wrong, to be dismissed out of hand.

"Irrationals" (literally, "no-ratio") cannot be expressed as a ratio of two numbers. For example, the irrational "pi" (a relationship between diameter and circumference) becomes an endless series of digits, 3.14159265... on and on forever. Because it is an irrational, "pi" cannot be expressed as a neat, tidy ratio-fraction, like 1/4 or 0.25 -- irrationals don't work that way.

The "rationals" represent "countable," "listable" infinities, but the domain of the "irrationals" is a much, much, much larger field of "uncountable," "unlistable" infinities.

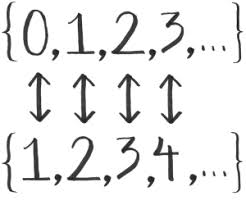
the terms "countable" and "listable" refer to one-to-one correspondence 

We are indebted to Georg Cantor for work in this area. You'll want to read about his discoveries.

First, let's look at how a 'listable," "countable," infinity works:

Notice the one-to-one correspondence. On the top we have the set of whole numbers, and on the bottom we have the set of natural or counting numbers.

We understand that both sets of numbers go on forever. However, in this infinite progression, there will always be a matched one-to-one correspondence. These are called, or are considered to be, with a wink, "countable" or "listable" infinities.

But hold on, we say! How could this be? The bottom row, the counting numbers, begins with 1. The top row, it would appear, has one more element in the set -- it begins with 0; and so, "obviously," we insist, these sets cannot be equal, and cannot be equally matched in one-to-one correspondence. And yet these two sets are matched in one-to-one correspondence. The two sets have an equal number of elements and represent infinities of equal size.

But the "weirdness" has hardly begun.

Here's another example:

It's the same chart as above, but I'm going to ask you to mentally change it. We'll keep the whole numbers on top, but on the bottom take away the counting numbers and insert the squares of each number from the top; therefore, 0 would be matched with 0 (0 x 0), 1 would be matched with 1 (1 x 1), 2 would be matched with 4 (2 x 2), 3 would be matched with 9 (3 x 3) ... continuing on forever.

Both sets are equal in terms of set-elements and represent equally-sized "countable" infinities.

Let's change the chart again. This time, on the lower row, insert additions of 1 trillion: 0 would be matched with 1 trillion, 1 would be matched with 2 trillion, 2 would be matched with 3 trillion ... continuing on forever.

Both sets are equal in terms of elements in the sets; both are "countable" or "listable" infinities.

Editor's note: Basically, we could use any listable series on the bottom, each of which might be in one-to-one correspondence with the top. As we begin to fathom, the listable infinities are not small; however, we'll soon see them in a new light.

Galileo did his own thought-experiment with this. He used the set of all integers on the top and the set of their squares on the bottom.

Galileo said that the old 3-D terminology and way of looking at the world doesn't apply to infinity

Dr. Adler: "What Galileo points out about two infinite quantities seems to hold for an infinite and a finite quantity (meaning, the one-to-one correspondence of both sets is a valid way of determining equality, even though it may seem non-intuitive to us). He asks us to consider the totality of all integers (which is infinite) and the totality of their squares (which is also infinite). On the one hand there appear to be as many squares as there are integers; on the other hand, the totality of integers includes all the squares. Precisely because 'the number of squares is not less than the totality of all numbers, nor the latter greater than the former' (i.e., both sets are equal in terms of elements in their sets) Galileo insists that 'the attributes equal, greater, and less are not applicable to infinite but only to finite quantities'."

On the level of "countable infinities," within the domain of the rationals, there seems to be no end to the matching and pairing, the one-to-one correspondence, of number systems. And yet, all this infinitude is but a speck, and less than a speck, compared to the gigantic, and beyond gigantic, magnitude of the "uncountable infinities."

the awesome and incredible world of mega-behemoth 'uncountable infinities'

We've caught a tiny glimpse of the "countable" infinities. These are infinities, "countable" infinities, the elements of which, albeit theoretically, might be put on a list.

But there's an order of magnitude among the infinities, so expansive and commanding, so vast and undefined, that no list could ever begin to contain or speak to its elements -- not even theoretically. It is an unfathomable domain so incalculably large that, as stated earlier, we could throw away all the "countable infinities" buried within the real number line, and not even notice they're gone.

the 'countables', like an unnoticed missing speck of dust in the universe, are immeasurably smaller than the 'uncountables'

Georg Cantor (1845-1918), one of the greatest mathematical minds of history, is credited with the discovery of the 'uncountable infinities.'

Cantor's work was deemed to be so disturbing, so iconoclastic, to orthodox science and mathematics, that, for some time, his "heresy" was rejected by the cult-priests of establishment academia. Tragically, in poverty and suffering, he died in a mental institution, rejected and reviled by small minds around him.

Cantor's Diagonal Method

You'll want to do your own research on Cantor's work. It will be my purpose here to offer only the briefest introduction, but, I hope, a meaningful one.

We've seen "countable infinities", but how could it be determined that an "uncountable" infinity might exist? Cantor's method of discovery is simple in essence, as all truly great discoveries are. I will attempt an abbreviated explanation.

how do we know that the 'countable' infinite sets of the 'rationals' are smaller infinities than the 'uncountable' 'irrationals'

Let's make our thought-experiment as simple as possible by considering only the fractions, between 0 and 1. Sounds manageable. But we'll see.

We know that on a "countable list" fractions might be made smaller and smaller; all we need do is keep dividing by 2 (or any other number, but let's not confuse ourselves right now). And with this method of dividing by 2, we could "fill up our list" between 0 and 1.

This is a "countable list," and while, given enough time, all elements of that list would reveal themselves, we remember that the "uncountable infinities," for our purposes at the moment between 0 and 1, have a reputation of being much larger than their "countable" brethren. The "rationals" might be neatly put on a list, but not the "irrationals," and there're a whole lot more "irrationals" between 0 and 1 than the "rationals" ever thought about.

Here's what Cantor did to show this. He created a series of numbers -- not these exactly, but this factoid doesn't matter right now; it was similar to this:

The vertical blue line, on the left, numbers the rows: row #1, row #2, row #3, and so on, and it will go down the list this way forever.

Each row is associated with a certain number. Row #1 is linked to 0.112452... and this number, stretching infinitely to the right, will be a very long number, an infinite number of digits.

Now, you might ask, where do these numbers come from, and shouldn't it be important which numbers we use for this investigation? We will discover that the number-sequence or the order does not matter.

Cantor's purpose was to show that no matter how long the list might be, no matter how many numbers we put on this infinite list, there would be some numbers that would never be on the list.

Editor's note: Right here we have the difference between the "countables" and the "uncountables." The "countables" might be formulated as a list onto which all of its elements will eventually appear; but there's no way to do the same for the "uncountables" - you can keep adding numbers to this latter list, I mean any old number on the list, as fast as they pop into your head, and do this forever, and still there would be an "infinite infinity" of numbers that would never, ever make it onto the list.

What would this mean? Well, let's restate: It would mean that we're not dealing with a "countable" or "listable" infinity. Remember, the list of natural or whole numbers, while infinite, is still countable. We know that their elements will eventually all be "on the list." All of the "rationals" will be on the list. But it doesn't work that way with the "irrationals."

To get the hang of this, let's focus on row #1...

0.112452... is a perfectly respectable number and there's no reason why it shouldn't be on this list, especially a list that's infinitely long.

But here's what Cantor saw: 0.112452... is the first number on the list, and there's one thing that's perfectly clear - it's on the list.

I don't mean to use double-talk, but when I say 0.112452... is on the list we can know that 0.112452... is a member of a "countable" infinity. How do we know? - because it's on a list, and the "uncountables" will not be on the list.

This is actually a very important point. Ok, we're just on row 1, and it's only the first number, but trust me when I say that the important thing we know so far is that 0.112452... is on the list, which means that any "uncountable list" will not contain this number. And so we say, "since I know that 0.112452 is on the list, I can think of a number that's not on the list" - which is another way of saying, "I can think of a number that would be an element of an "uncountable" infinity.

I'll explain the procedure.

Here again is our first number on the list: 0.112452... We notice the "1" that's in red. But let's construct our own number now, a new number, one that won't be on the list, and we'll do this by adding a 1. Why are we doing this? - it's our first step toward creating a number that's not on the infinite "countable" list.

Since we're focusing on a number-range between 0 and 1, we'll keep the 0, the first digit, which is left of the decimal point. But now let's replace the red "1" on the infinite list with our own number by adding 1. Now we have two digits in our "new number," 0.2...

We started with 0.112452... and now, by a simple algorithm of adding a 1, we have 0.2...

It doesn't matter what comes after our "2" -- it could be a string of any numbers that we like; and it doesn't matter what comes after the red "1," because one thing's for sure already, our new number 0.2... is different from 0.112452...

As we methodically proceed down the infinite list, as we encounter and evaluate each row, every time, in each case, our newly-constructed number will be different from the preceding numbers found on all rows encountered to that point. Here are a few more examples to make the process more clear.

Let's look at row #2:

Notice that the green 4 is diagonally positioned to the red 1; hence the title, "Cantor's diagonal method." If we add 1 to the green 4, our newly-constructed and growing "uncountable" number will be 0.25...

It doesn't matter, in reference to these first two rows, what comes after 0.25... and it doesn't matter what comes after the green 4; all that matters, right now, is that we've created a number, 0.25..., that is different from numbers found on the first two rows.

One more time, to belabor the point, let's move to row #3...

We apply the same procedure, adding 1 to the next-in-line diagonally chosen yellow 3, and now our newly-constructed and growing "uncountable" number reads 0.254...

Again, it doesn't matter, in reference to these first three rows, what comes after 0.254... nor does it matter what comes after the yellow 3. What matters is that we've now constructed a number -- 0.254... -- that's not on "the list" of the first three rows.

And as we continue down this infinite list, diagonally selecting an offering from each row, and adding 1 to it, we will be constructing an infinitely long number whose primary characteristic, for our purposes, is that of not being on "the list." No matter how long this infinite list might become -- it could wrap itself around the universe an infinite number of times -- our newly-constructed number will not be on that very long list of numbers.

Georg Cantor helps us to understand that some infinite lists are bigger than other infinite lists - because some lists are "uncountable" and "unlistable," that is, some infinities are bigger than other infinities.

how big are these 'uncountable' infinities

I think it's above our current pay-grade to fathom this question, but consider this.

We added, on a "diagonal" basis,  a simple 1 to each row. But we could have added 2, or 3, or 7,684.659 -- if you see what I mean. Or, we might have constructed our "new uncountable number" by subtracting, dividing, or multiplying, or some other (infinitely varied) combination of mathematical operations; for example, "first divide by 3, then multiple by 47, then take the square root"; the possibilities are endless. The fact is, there are an infinite number of methods by which we might create an infinite number of "newly-constructed numbers" not on the list.

Editor's note: Not only are the potential "new diagonals" infinite in number, but the methods, too, by which these "hidden gaps" are produced are also infinitely varied. No wonder Cantor's math-peers felt their sanity under attack to consider the implications.

Of course, there's also the issue of purview relative to our search. We limited the scope of our investigation to irrationals between 0 and 1. Sounds harmless enough, so well contained, such a baby step. Until we're jerked into a vision of a smidgeon's worth of what's really going on here.

within each gradation of 0.1 -- or half-step, or, indeed, any part, thereof -- lies undiscovered realms, uncharted, even unknowable, infinities, incalculably larger than those of the entire rational number line

Instead of 0 to 1, how about 0 to 0.1, or 0 to 0.01, or 0 to 0.001, etc., etc. And let's not leave the negative numbers out of the party: 0 to -1, and 0 to -0.1, and 0 to -0.01, and 0 to -0.001, etc, etc. All we did in each case was to move a tiny decimal point. Hardly worth a notice, we say.

But, all of the uncharted infinity between 0 and 1 is answered by an equally bewildering blizzard of "uncountable" infinities; of infinities within infinities between each nano-section; of ever-smaller, diminishing, and receding kingdoms of quantification; all of which approach, but will never actually touch, zero -- all this, within the short step of 0 to 1! But it's not just 0 to 1 or 0 to -1. What about all the other fiefdoms? We can't even begin to pierce the dense fog of the infinity-realms, positive or negative, within 0 to 2, or 0 to 3, or 0 to 10, or to 1000, or to 1,000,000,000, on and on, without boundary.

Editor's note: A physicist-mathematician friend of mine said that Cantor's Diagonal Method is great, but it would help to simplify things if we just used 0's and 1's in the rows of numbers. This is brilliant on my friend's part. Look at that chart again:

Take away most of those digits and just use differently sequenced 0's and 1's. With this method, as we move diagonally down the rows, all we need do, when we construct our "uncountable" new number, is to change a digit into a 0 or a 1, depending on what is found. Imagine that! This is a whole new layer of infinite complexity, built around an infinite layering of 0's and 1's. But, I should have said to my friend, why stop with 0's and 1's? We can build the whole thing with an interplay of 1's and 2's, or 3's and 4's, or 1's and 3's, or some fractions, or 10,453's and 10,454's! All  this is beyond unfathomable in terms of depth, wonder, and mystery.

In the essay, "What Is Mathematics?" we discussed how math might represent aspects of reality. Do these "infinities upon infinities" reveal, or hint at, something of the splendor and complexity of our godlike, unlimited human potential to be played out on an eternal cosmic stage?

We call it "weird" because we're limited right now, operating in a fog at midnight, unable to see who we really are or the nature of reality.

III. Dr. William Barclay's explanation of the New Testament Greek word for 'eternal' life 

Please follow this link to Dr. Barclay's writing. Essentially, the classical meaning of the Greek word for "eternal" life does not primarily refer to endless duration of living but to quality of life, that is, to live life on the level of "the gods."

IV. Eckhart Tolle and the 'eternal now' 

The work of Eckhart Tolle is often presented on the Word Gems site. His writings present, in modern terminology, a wisdom of the East which has been lost, or never acquired, for us in the West.

Paramount among his teachings are the concepts of "the present moment" and the "eternal now." These are very much in line with Eternity definition #2 (see above).

V. Conclusion and Summary Thoughts  

Historically, we find that the two "great ideas," Eternity and Infinity -- concepts of the "endless" and "limitless," revolving about two primary definitions -- eventually part ways. Infinity later distinguishes itself from Eternity by focusing upon the mathematical illimitable.

A major portion of this discussion over the centuries has centered not upon "time" but "being," that of, God's eternal or infinite being and essence. The Churchmen felt that God is perfect and complete in all aspects of being and therefore, they said, God cannot change. However, many thinkers and mystics today disagree with this conclusion, in that, all of us, "made in the image," linked to God, experiencing so much as we do, contribute to God's experience. One thinker has stated that if, indeed, God were truly all knowing, absolutely omniscient, replete with every factoid in the universe, God could not think at all, as there would be nothing to think about, nothing to mentally create, and no new understanding possible, with all knowledge immediately present.

Regarding the issue of time, C.S. Lewis once said that we're continually shocked by temporal things: "I can't believe that so many years have passed"; or "Is little Johnny grown up already? The last time I saw him he was just this high!" It's as if, in all of this sense of shock, Lewis mused, we were not made for time, but for a timeless world.

Everything that has a beginning is also subject to an ending.

But there exists a domain beyond the reach of time’s degradation. There, things simply exist, eternally, have always been, have no opposite, no duality, and do not suffer loss.

And I like Dr. Adler's comment on what seems to be our unbounded destiny:

"If man’s restless search for knowledge and happiness can be quieted only by the possession of the infinite truth and goodness of God, then man’s intellect and will must somehow be as infinite in nature as they are in tendency.”

Georg Cantor's work with "uncountable" infinities, that some infinities are bigger than others, truly, is one of the mammoth discoveries of mathematics. However, a question does arise: Is the mathematics of infinity "created" or "discovered"? We've discussed this elsewhere.

Much of mathematics is clearly derived from the natural world, but when it comes to concepts of infinity, especially the "uncountable" sort, we cannot be certain that this aspect of mathematics mirrors our 3-D finite world. Our universe will one day grow cold, with every star burning out, in about 100 billion years - this means our universe has limits; as such, the mega-behemoth "uncountable" infinities seem to lack proper expression here, there's not enough elbow room in our "too small to stand up in" little universe.

Cantor's vision of infinity might tap into aspects of "the illimitable" germane only to other coming worlds and dimensions. This is all very mysterious. Despite our present mortality, we do, in fact, feel an element of the eternal within our deepest persons.

We are all headed for Summerland where time, for most events and activities, still flows somewhat the same as it does on Earth; however, reports indicate that time there might also flow differently; and, in some places, might seem to stand still in that proverbial "eternal now." As we learn from Eckhart Tolle, and as I have personally experienced, there is a domain, deep within the "true self," wherein "the eternal now" already lives and might be accessed.

the universe has limits, but we do not

I like Father Benson's assessment of our capacities: "no discernible upper limit" to our human potential. This is affirmed by Spirit Guides. The statement "no upper limit" takes us very close to, and crosses the line into, notions of eternity and infinity. It's odd that the 3-D universe itself does have limits to contend with in its future, but we, "made in the image," do not! - is this akin to an "uncountable infinity"?

I think C.S. Lewis was right: Eternity and Infinity have been written into "our spiritual DNA," and we're often shocked by an assault of time which seems unnatural to us.

We'll be investigating these questions, and many related issues, for a long time to come. I hesitate to use the phrase "for an infinite time to come" due to certain overuse in this writing. And, though it might be infinite, we certainly wouldn't want to make an alliance with one of those disreputable, hardly-worth-mentioning "countable infinities."